So, we just discussed all of the logic behind it, so let us just run the example normally and get the data.
Running The Algorithm
Pre-Processing
# Foreign trade subset
f_trade <- TradeData0014[TradeData0014$exporter != TradeData0014$importer,]
# Normalize trade data to unit interval
f_trade$trade <- f_trade$trade / max(f_trade$trade)
# classify FEs for components to be absorbed (finding variable interactions)
f_trade$exp_year <- interaction(f_trade$expcode, f_trade$year)
f_trade$imp_year <- interaction(f_trade$impcode, f_trade$year)
f_trade$pair <- interaction(f_trade$impcode, f_trade$expcode)
# Fit generalized linear model based on specifications
partials <- feglm(
formula = trade ~ eu_enlargement + other_fta | exp_year + imp_year + pair,
data = f_trade,
family = poisson()
)$coefficient # We just need the coefficients for computation
# Sort trade matrix to make it easier to find imp/exp pairs
t_trade <- TradeData0014[order(
TradeData0014$exporter,
TradeData0014$importer,
TradeData0014$year
),]
t_trade$eu_effect <- NA # this creates a new column with the partial effect of EU membership for new EU pairs
i <- 1
# Effect of EU entrance on country based on partial, if entry happened
invisible(by(t_trade, list(t_trade$expcode, t_trade$impcode), function(row) {
# Was a new EU pair created within time span?
t_trade[i:(i+nrow(row)-1), "eu_effect"] <<- diff(row$eu_enlargement, lag=nrow(row)-1)
i <<- i + nrow(row)
}))
# If added to EU, give it the computed partial eu_enlargement coefficient as the effect
t_trade$eu_effect = t_trade$eu_effect * partials[1]
# Data to be finally fed to the function
data <- t_trade[t_trade$year == 2000,] # In example, 1892 Entries, 5676 removed
head(data)
#> exporter importer expcode impcode year trade eu_enlargement other_fta
#> 1 AUS AUS 1 1 2000 704777.47410 0 1
#> 5 AUS AUT 1 2 2000 61.95446 0 0
#> 9 AUS BEL 1 3 2000 345.46746 0 0
#> 13 AUS BGR 1 4 2000 5.71090 0 0
#> 17 AUS BRA 1 5 2000 557.74257 0 0
#> 21 AUS CAN 1 6 2000 1583.67895 0 0
#> FTA eu_effect
#> 1 1 0
#> 5 0 0
#> 9 0 0
#> 13 0 0
#> 17 0 0
#> 21 0 0Running Actual Computations
## Difference between w_mult and w_o_mult is how trade balance is considered
## mult = TRUE assumes multiplicative trade balances; false assumes additive
w_mult <- ge_gravity(
exp_id = data$expcode, # Origin country associated with each observation
imp_id = data$impcode, # Destination country associated with each observation
flows = data$trade, # Observed trade flows in the data for the year being used as the baseline
beta = data$eu_effect, # “Partial” change in trade, obtained as coefficient from gravity estimation
theta = 4, # Trade elasticity
mult = TRUE, # Assume trade balance is a multiplicative component of national expenditure
data = data
)
w_o_mult <- ge_gravity(
exp_id = data$expcode, # Origin country associated with each observation
imp_id = data$impcode, # Destination country associated with each observation
flows = data$trade, # Observed trade flows in the data for the year being used as the baseline
beta = data$eu_effect, # “Partial” change in trade, obtained as coefficient from gravity estimation
theta = 4, # Trade elasticity
mult = FALSE, # Assume trade balance is an additive component of national expenditure
data = data
)Final results without multiplicative option
head(w_o_mult)
#> exporter importer expcode impcode year trade eu_enlargement other_fta
#> 1 AUS AUS 1 1 2000 704777.47410 0 1
#> 5 AUS AUT 1 2 2000 61.95446 0 0
#> 9 AUS BEL 1 3 2000 345.46746 0 0
#> 13 AUS BGR 1 4 2000 5.71090 0 0
#> 17 AUS BRA 1 5 2000 557.74257 0 0
#> 21 AUS CAN 1 6 2000 1583.67895 0 0
#> FTA eu_effect new_trade welfare real_wage nom_wage price_index
#> 1 1 0 7.047388e+05 0.9999938 0.9999945 0.9999236 0.9999292
#> 5 0 0 6.200899e+01 0.9999938 0.9999945 0.9999236 0.9999292
#> 9 0 0 3.454304e+02 0.9999938 0.9999945 0.9999236 0.9999292
#> 13 0 0 5.302484e+00 0.9999938 0.9999945 0.9999236 0.9999292
#> 17 0 0 5.576790e+02 0.9999938 0.9999945 0.9999236 0.9999292
#> 21 0 0 1.583680e+03 0.9999938 0.9999945 0.9999236 0.9999292Final results with multiplicative option
head(w_mult)
#> exporter importer expcode impcode year trade eu_enlargement other_fta
#> 1 AUS AUS 1 1 2000 704777.47410 0 1
#> 5 AUS AUT 1 2 2000 61.95446 0 0
#> 9 AUS BEL 1 3 2000 345.46746 0 0
#> 13 AUS BGR 1 4 2000 5.71090 0 0
#> 17 AUS BRA 1 5 2000 557.74257 0 0
#> 21 AUS CAN 1 6 2000 1583.67895 0 0
#> FTA eu_effect new_trade welfare real_wage nom_wage price_index
#> 1 1 0 7.047407e+05 0.9999948 0.9999948 0.9999268 0.9999321
#> 5 0 0 6.200460e+01 0.9999948 0.9999948 0.9999268 0.9999321
#> 9 0 0 3.454142e+02 0.9999948 0.9999948 0.9999268 0.9999321
#> 13 0 0 5.261708e+00 0.9999948 0.9999948 0.9999268 0.9999321
#> 17 0 0 5.576743e+02 0.9999948 0.9999948 0.9999268 0.9999321
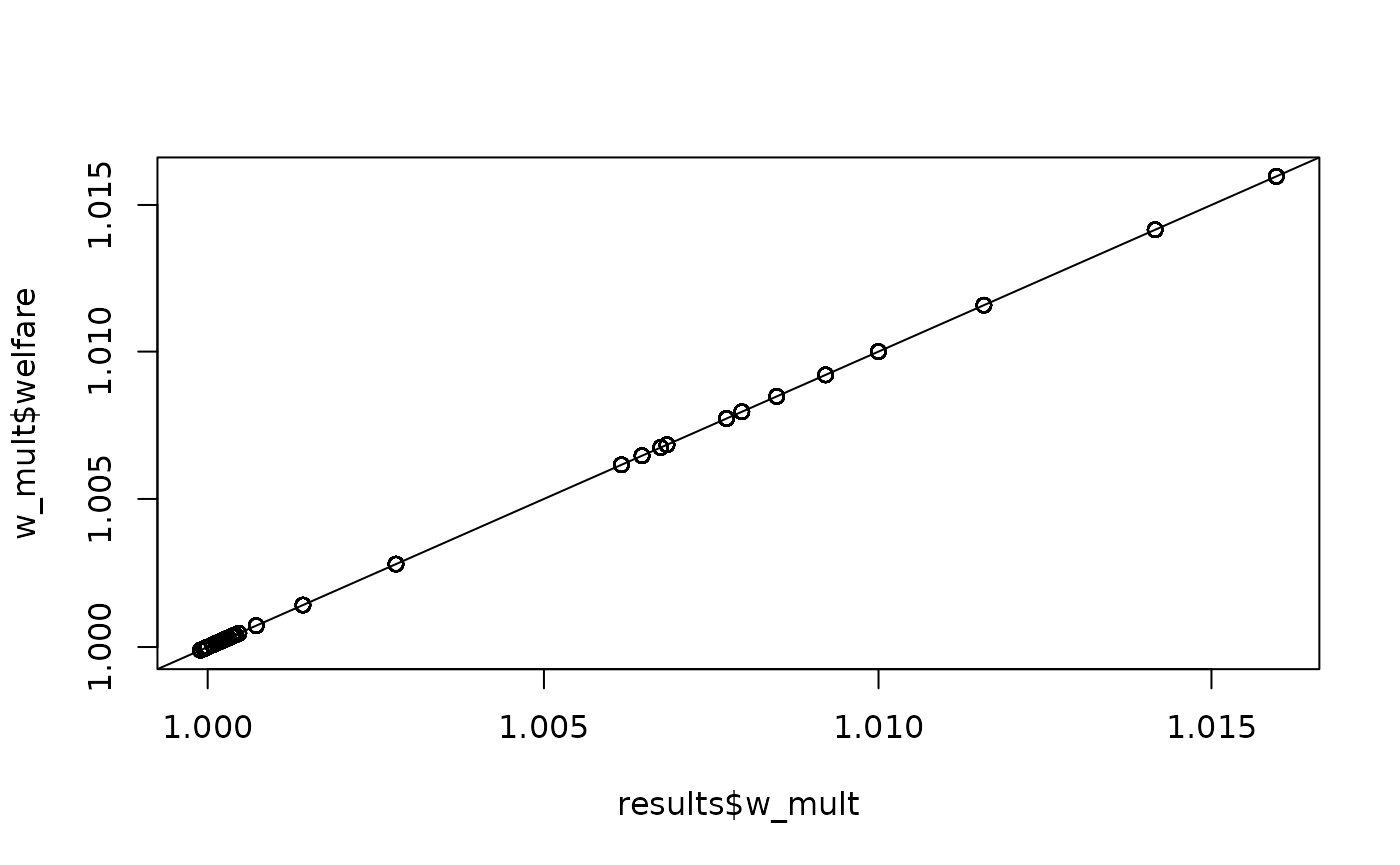
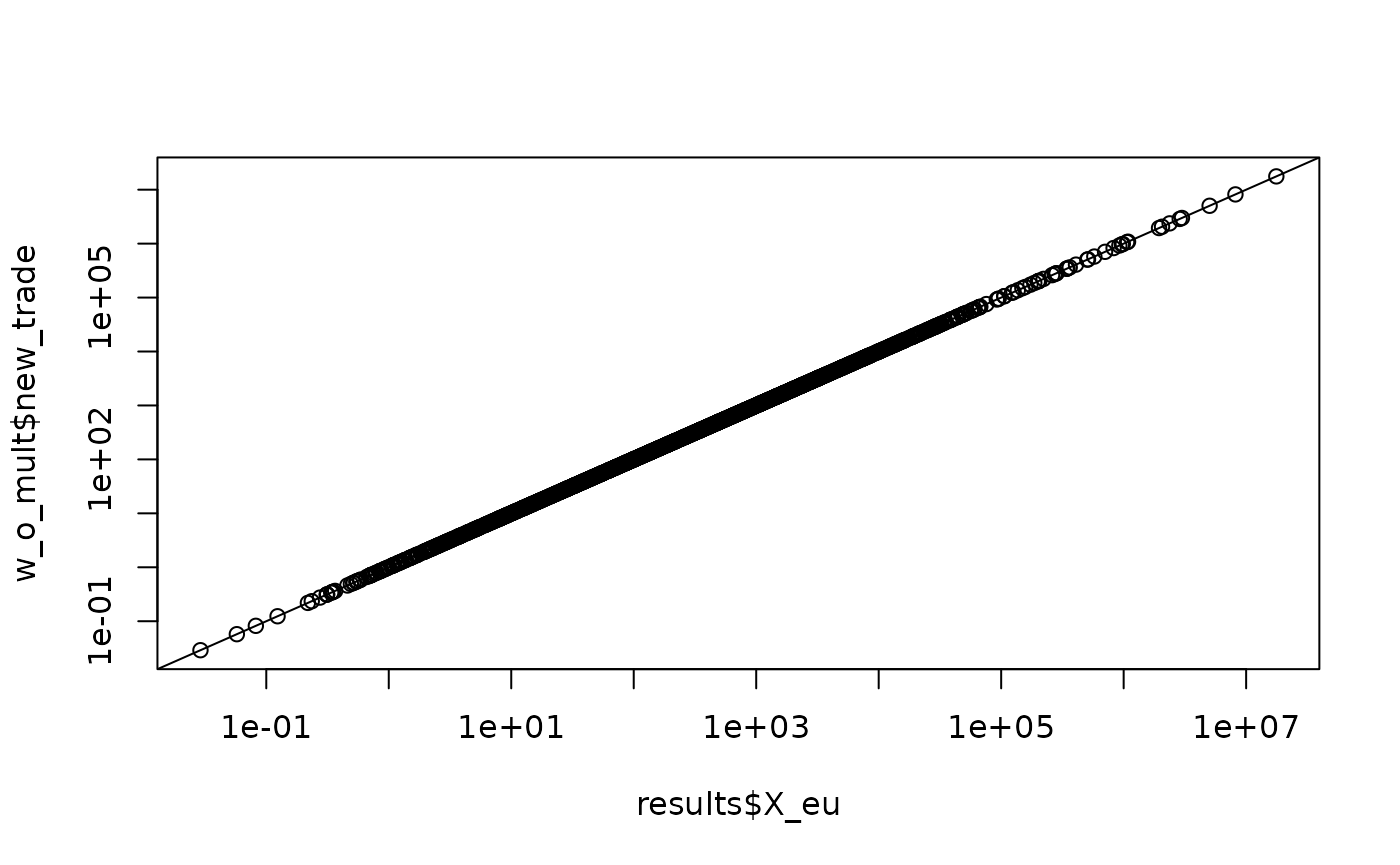
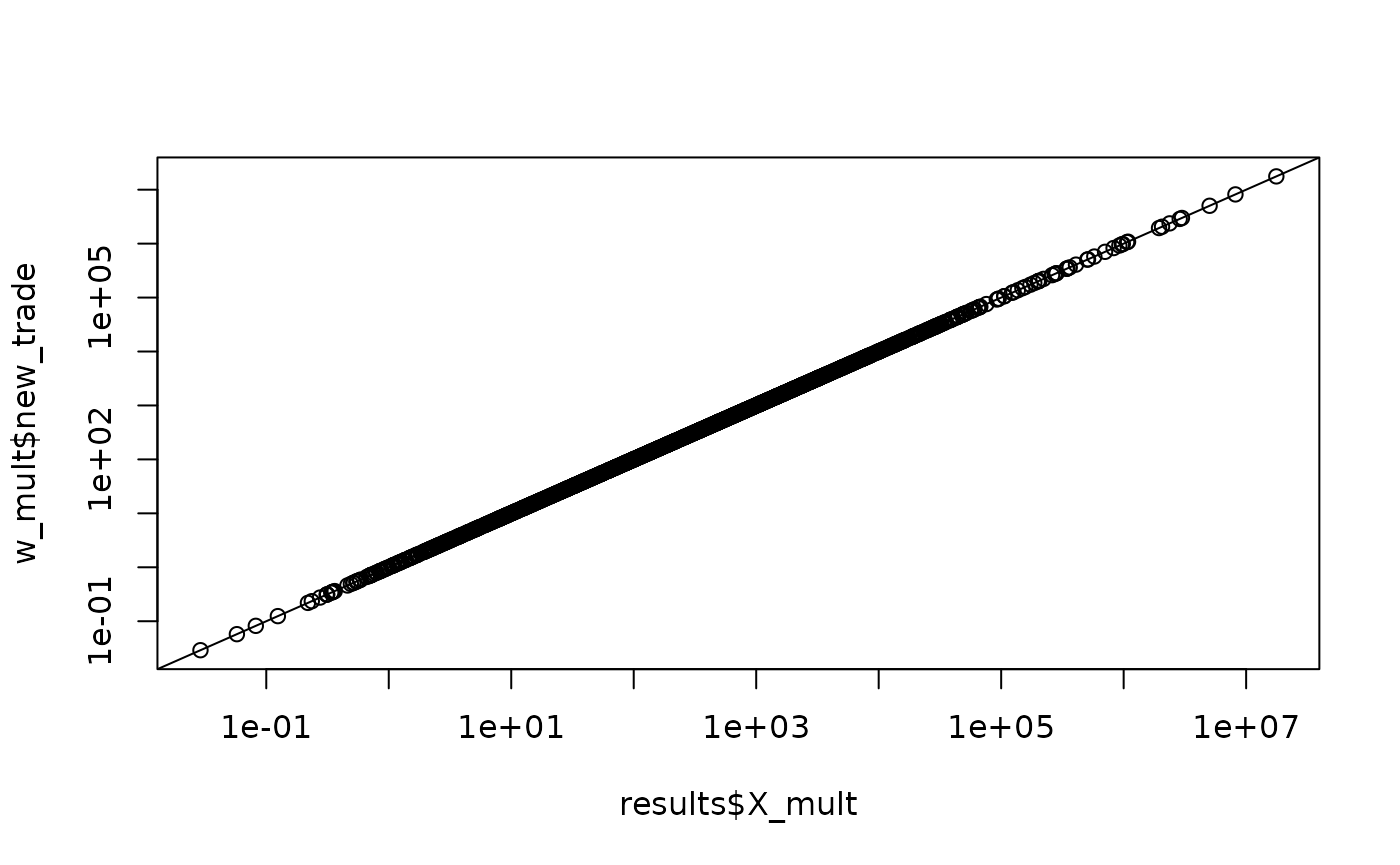
#> 21 0 0 1.583683e+03 0.9999948 0.9999948 0.9999268 0.9999321Comparison with Stata Counterpart
As mentioned, this package is intended to mimic the functionality of the Stata package of the same name, so we will do a quick comparison of this data relative to the same computation from the Stata counterpart.
Before running comparisons, we need to slightly modify the results data to sync with our new format.
# Notice that the Stata counterpart returned all years with a sparse
# selection labeled with computed values. Ours just returns the new data
# by default or tags it onto the data provided in the `data` parameter.
# To make it sync, just extract a year.
results <- TradeData0014_Results[TradeData0014_Results$year == 2000, ]
head(results)
#> exporter importer expcode impcode year trade eu_enlargement other_fta
#> 1 AUS AUS 1 1 2000 704777.47410 0 1
#> 5 AUS AUT 1 2 2000 61.95446 0 0
#> 9 AUS BEL 1 3 2000 345.46746 0 0
#> 13 AUS BGR 1 4 2000 5.71090 0 0
#> 17 AUS BRA 1 5 2000 557.74257 0 0
#> 21 AUS CAN 1 6 2000 1583.67895 0 0
#> FTA new_eu_pair eu_effect w_eu X_eu w_mult X_mult
#> 1 1 0 0 0.9999938 7.047388e+05 0.9999948 7.047407e+05
#> 5 0 0 0 0.9999938 6.200899e+01 0.9999948 6.200460e+01
#> 9 0 0 0 0.9999938 3.454304e+02 0.9999948 3.454142e+02
#> 13 0 0 0 0.9999938 5.302484e+00 0.9999948 5.261708e+00
#> 17 0 0 0 0.9999938 5.576790e+02 0.9999948 5.576743e+02
#> 21 0 0 0 0.9999938 1.583680e+03 0.9999948 1.583683e+03Comparison of w_mult from stata results to the computed welfare change w/ multiplicative trade imbalances