GE_Gravity Theory, Logic, Testing, and Comparison

This is a compiled RMD file describing a GEGravity in more depth. For parameterizations and basic description, see the documentation i.e. help(ge_gravity). This is more of an extension to the formal documentation to keep the help command from being overbloated.

This overarching file contains all of the contents of theory.Rmd, example.Rmd, logic.Rmd, and compare.Rmd, almost in that order. To see the smaller version, please check out ge_gravity_rmd

Background

As a typical application, consider the following model for international trade flows: \[X_{ij} =\frac{A_{i}w_{i}^{-\theta}\tau_{ij}^{-\theta}}{\sum_{k}A_{k}w_{k}^{-\theta}\tau_{kj}^{-\theta}}E_{j}\]

\(X_{ij}\) are international trade flows. \(i\) and \(j\) are indices for origin and destination. \(E_{j} \equiv \sum_{i}X_{ij}\) is total expenditure (also equal to the sum of the value of shipments across all origins). \(A_{i}\) is a measure of the level of technology in each origin \(i\), \(w_{i}\) is the production cost, and \(\tau_{ij} > 1\) is an iceberg trade cost. The model assumes that goods received from different origins are imperfectly substitutable and that the degree of substitutability is governed by \(\theta > 0\), which serves as a trade elasticity. Labor, \(L_{i}\), is assumed to be the only factor of production. Trade imbalances, treated as exogenously given, are accounted for as an additive component of expenditure. Thus, we can also write national expenditure as the sum of labor income and the national trade deficit/surplus: \(E_{j} = w_{j}L_{j} + D_{j}\).

To obtain the effects of changes in trade policies on trade (i.e., holding all wages fixed), a standard approach is to estimate using structural gravity. For example, if we have a panel of trading countries and we want to know the “average partial effect” of FTAs on trade, we can estimate the following “three-way” gravity regression:

\[X_{ijt} =\exp\left[\ln\alpha_{it}+\ln\alpha_{jt}+\ln\alpha_{ij}+\beta\times FTA_{ijt}\right]+e_{ijt},\]

As discussed in Yotov, Piermartini, Monteiro, & Larch (2016), the estimated \(\beta\) from this specification tells us how much trade would increase on average between any pair of countries that sign an FTA if we hold fixed all the endogenous variables in the model. Or, put in more structural terms, it tells us the direct trade impact of the reduction in trade barriers associated with an FTA: \(\beta=-\theta\Delta\ln\tau_{ijt}\).

However, often the real goal is to compute changes in real wages, welfare, and/or trade volumes as a result of a change in trade frictions. In general equilibrium, the value of a country’s shipments across all destinations must add up to its labor income (\(Y_{i} \equiv w_{i}L_{i} = \sum_{j}X_{ij}.\)) In other words, we must have that

\[w_{i}L_{i} =\sum_{j} \frac{A_{i}w_{i}^{-\theta}\tau_{ij}^{-\theta}} {\sum_{k}A_{k}w_{k}^{-\theta}\tau_{kj}^{-\theta}} \left(w_{j}L_{j}+D_{j}\right) \quad \forall i.\]

This equation pins down each country’s wages (subject to a normalization) as a function of how easily it can sell to markets with high levels of demand. Similarly, notice that we can express the effective price level in each country, \(P_{j} \equiv \left[\sum_{k}A_{k}w_{k}^{-\theta}\tau_{kj}^{-\theta}\right]^{-1/\theta}\), as a function of how easily a country can buy from producers with high technology levels and low production costs. These linkages are both intuitive and general; they can be found in many different trade models typically used for GE analysis.

A useful point about the system of equations in wages is that it can be solved in “changes” (as opposed to solving it in levels). Adopting the notation of Dekle, Eaton, & Kortum (2007), let a “hat” over a variable denote the change in that variable resulting from a policy change (e.g., \(\widehat{w}_{i}\equiv w_{i}^{\prime}/w_{i}\) gives the change in \(i\)’s wage level.) Noting that \(\widehat{\tau}_{ij}^{-\theta}=e^{\beta\times FTA_{ij}}\), the “equilibrium in changes” version of wages can be written as:

\[Y_{i}\widehat{w}_{i} = \widehat{w}_{i}^{-\theta} \sum_{j}\frac{\pi_{ij}\cdot e^{\beta \times FTA_{ij}}} {\widehat{P}_{j}^{-\theta}} \cdot\left(Y_{j}\widehat{w}_{j} + D_{j}\right) \quad\forall i,\]

where \(\pi_{ij}\equiv X_{ij}/E_{j}\) is a bilateral trade share and \(\widehat{P}_{j}\equiv\left[\sum_{k}\pi_{kj}\widehat{w}_{k}^{-\theta}e^{\beta\times FTA_{kj}}\right]^{-1/\theta}\) describes the change in price levels in each country. Notice this equation can be solved without knowledge of technology levels, endowments, initial trade frictions, or initial wages. All that is needed are trade volumes, national output and expenditure levels, and a value for the trade elasticity \(\theta\).

Once changes in wages are known, GE changes in welfare, real wages, and trade volumes are given respectively by: \[ \textbf{GE Welfare Impact}:\quad \widehat{W}_{i}=\widehat{E}_{i}/\widehat{P}_{i}\\ \\ \textbf{GE Real Wage Impact}:\quad \widehat{rw}_{ij}=\widehat{w}_{i}/\widehat{P}_{i},\\ \textbf{GE Trade Impact}:\quad \widehat{X}_{ij}=\frac{\widehat{w}_{i}^{-\theta}e^{\beta\times FTA_{ij}}}{\widehat{P}_{j}^{-\theta}}\cdot\widehat{E}_{j} \] where the change in national expenditure, \(\widehat{E}_{i}\), is given by \((Y_{i}\widehat{w}_{i} + D_{i}) / E_{i}\). Because trade volumes are nominal quantities, there is one normalization needed. For this, the algorithm assumes that total world output is the same across both the baseline and the counterfactual (i.e., \(\sum_{i}Y_{i}\widehat{w}_{i} = \sum_{i}Y_{i}\).) The precise method used to solve the model is described further below.

Algorithm

While there are several ways to solve for counterfactuals in the above model, the simplest approach is arguably a fixed point algorithm that repeatedly iterates on the equilibrium conditions of the model. There are numerous ways to implement such an algorithm, but the approach used in Baier, Yotov, & Zylkin (2019) is especially simple to program. We first initialize \(\widehat{w}_{i}=\widehat{P}_{i}^{-\theta}=1\) \(\forall i\) and \(E_{i}^{\prime}=E_{i}\)\(\forall i\). The iteration loop then requires only 4 steps:

Update \(\widehat{w}_{i}\) \(\forall\) \(i\) one time using \[\widehat{w}_{i} = \left[Y_{i}^{-1}\sum_{j}\frac{\pi_{ij}\cdot e^{\beta\times FTA_{ij}}}{\widehat{P}_{j}^{-\theta}}\cdot E_{j}^{\prime}\right]^{\frac{1}{1+\theta}}\quad\forall i.\]
Normalize all wages so that world output stays fixed: \(\sum_{i}Y_{i}\widehat{w}_{i}=\sum_{i}Y_{i}\).
Update \(\widehat{P}_{j}^{-\theta}=\left[\sum_{k}\pi_{kj}\widehat{w}_{k}^{-\theta}e^{b\times FTA_{kj}}\right]\) \(\forall\) \(j\).
Update \(E_{j}^{\prime}=Y_{j}\widehat{w}_{j}+D_{j}\) \(\forall\) \(j\).

(Repeat steps 1-4 until convergence.)

This algorithm is very similar to one previously made available by Head & Mayer (2014), but takes a slightly more streamlined approach to updating wages in step 1. It should generally be very fast because it does not involve using a nonlinear solver.

Example

For an example, the package comes with example data TradeData0014. The data set consists of a panel of 44 countries trading with one another over the years 2000-2014. The trade data uses aggregated trade flows based on WIOD and information on FTAs is from the NSF-Kellogg database maintained by Scott Baier and Jeff Bergstrand. To find out more about the trade data, see Timmer, Dietzenbacher, Los, Stehrer, and de Vries (2015).

data(TradeData0014) # loads data included with package
head(TradeData0014) 
#>   exporter importer expcode impcode year        trade eu_enlargement other_fta
#> 1      AUS      AUS       1       1 2000 7.047775e+05              0         1
#> 2      AUS      AUS       1       1 2005 1.334877e+06              0         1
#> 3      AUS      AUS       1       1 2010 2.210350e+06              0         1
#> 4      AUS      AUS       1       1 2014 2.436575e+06              0         1
#> 5      AUS      AUT       1       2 2000 6.195446e+01              0         0
#> 6      AUS      AUT       1       2 2005 1.407591e+02              0         0
#>   FTA
#> 1   1
#> 2   1
#> 3   1
#> 4   1
#> 5   0
#> 6   0

Suppose the researcher wishes to use this data set to quantify general equilibrium trade and welfare effects of the EU enlargements that took place between 2000-2014. To first obtain the partial effects of these enlargements on trade flows, a PPML (Poisson pseudo-maximum likelihood) gravity specification may be used. Specifically, to obtain the “partial” estimates of the effects of EU enlargements on trade, we can use the following three-way gravity specification:

\[X_{ijt} = \exp\bigg[\ln(\alpha_{it}) + \ln(\alpha_{jt}) + \ln(\alpha_{ij}) + \beta \cdot FTA_{ijt}\bigg] + e_{ijt}\]

The Stata equivalent of this package uses the ppmlhdfe command created by Correia, Guimarães, & Zylkin (2019) to achieve this. In our example, we will use the ‘alpaca’ library by Amrei Stammann to do the same via the feglm (Fixed-Effect Generalized Linear Model) function.

library(alpaca)  # Needed for partial coefficients

# Generate foreign trade subset
f_trade <- TradeData0014[TradeData0014$exporter != TradeData0014$importer,]

# classify FEs for components to be absorbed (finding variable interactions)
f_trade$exp_year <- interaction(f_trade$expcode, f_trade$year)
f_trade$imp_year <- interaction(f_trade$impcode, f_trade$year)
f_trade$pair     <- interaction(f_trade$impcode, f_trade$expcode)

# Fit generalized linear model based on specifications
partials <- feglm(
  formula = trade ~ eu_enlargement + other_fta | exp_year + imp_year + pair,
  data    = f_trade,
  family  = poisson()
)$coefficient  # We just need the coefficients for computation

print(round(partials, 3))
#> eu_enlargement      other_fta 
#>          0.224         -0.037

In addition to estimating the effects of EU enlargements on new EU pairs, this example also controls for any other FTAs signed during the period. Each of these variables is coded as a dummy variable that becomes 1 when the agreement goes into effect for a given pair. The estimated coefficient for eu_enlargements is 0.224, implying that the expansion of the EU had an average partial effect of \(e^{0.224} − 1 = 25.1\%\) on trade between new EU members and existing members. With clustered standard errors, this estimate is statistically significant at the \(p < .01\) significance level.

Before proceeding, some further pre-processing is needed. Specifically, we need to supply the function with the partial effects of joining the EU estimated above for each of the appropriate pairs. To do this, we create a new variable whose value is either the eu_enlargement partial computed above or 0.

For Stata users, the Stata equivalent of this next step is:

sort exporter importer year
by exporter importer: gen new_eu_pair = (eu_enlargement[_N]-eu_enlargement[1])                   
by exporter importer: gen eu_effect = _b[eu_enlargement] * new_eu_pair

In R, we do the following:

# Sort matrix to make it easier to find imp/exp pairs
t_trade <- TradeData0014[order(
  TradeData0014$exporter,
  TradeData0014$importer,
  TradeData0014$year),
]

t_trade$new_eu_pair <- NA
t_trade$eu_effect   <- NA   # this creates a new column that will contain partial effect of EU membership for new EU pairs
i <- 1
# Effect of EU entrance on country based on partial, if entry happened
invisible(by(t_trade, list(t_trade$expcode, t_trade$impcode), function(row) {
  # Was a new EU pair created within time span?
  t_trade[i:(i+nrow(row)-1), "new_eu_pair"] <<- diff(row$eu_enlargement, lag=nrow(row)-1)
  i <<- i + nrow(row)
}))

# If added to EU, give it the computed partial eu_enlargement coefficient (0.224) as the effect
t_trade$eu_effect = t_trade$new_eu_pair * partials[1]

To finalize the data for the counterfactual, we will use the year 2000 as the baseline year. The data we will feed to the ‘ge_gravity’ command looks like this:

# Data to be finally fed to the function (we base the counterfactual on the year 2000.)
ge_baseline_data <- t_trade[t_trade$year == 2000,]   # In example, 1892 Entries, 5676 removed

# head(data) # First 10 rows
ge_baseline_data[sample(1:nrow(ge_baseline_data), 10),]  # 10 random rows
#>      exporter importer expcode impcode year      trade eu_enlargement other_fta
#> 6289      ROU      NOR      36      33 2000   70.42168              0         1
#> 2277      ESP      TUR      13      42 2000 1660.11632              0         1
#> 6077      PRT      ITA      35      24 2000  893.41356              1         0
#> 1873      DEU      LVA      11      29 2000  411.83237              0         1
#> 2433      EST      ROW      14      37 2000  499.42945              0         1
#> 5509      NLD      EST      32      14 2000   45.65391              0         1
#> 7549      TWN      SVN      43      40 2000   48.57555              0         0
#> 4345      JPN      MLT      25      31 2000   34.98560              0         0
#> 6589      RUS      HUN      38      20 2000 1749.76171              0         0
#> 6045      PRT      FRA      35      16 2000 2468.06835              1         0
#>      FTA new_eu_pair eu_effect
#> 6289   1           1  0.224249
#> 2277   1           0  0.000000
#> 6077   1           0  0.000000
#> 1873   1           1  0.224249
#> 2433   1           0  0.000000
#> 5509   1           1  0.224249
#> 7549   0           0  0.000000
#> 4345   0           0  0.000000
#> 6589   0           0  0.000000
#> 6045   1           0  0.000000

Now that we have the data we need, we can run the ‘ge_gravity’ function as follows:

ge_results <- ge_gravity(
  exp_id = ge_baseline_data$expcode,    # Origin country associated with each observation
  imp_id = ge_baseline_data$impcode,    # Destination country associated with each observation
  flows  = ge_baseline_data$trade,      # Observed trade flows in the data for the year being used as the baseline
  beta   = ge_baseline_data$eu_effect,  # “Partial” change in trade, obtained as coefficient from gravity estimation
  theta  = 4,               # Trade elasticity
  mult   = FALSE,           # Assume trade balance is an additive component of national expenditure
  data   = ge_baseline_data
)
ge_results[sample(1:nrow(ge_results), 10),c(1:2,5:6,12:16)] # 10 random rows
#>      exporter importer year        trade    new_trade   welfare real_wage
#> 6429      ROW      ITA 2000 49686.811375 49744.775334 0.9999777 0.9999755
#> 485       BEL      POL 2000  1205.238414  1474.227573 1.0003657 1.0003587
#> 5629      NLD      USA 2000 13529.090121 13517.603220 1.0003121 1.0003057
#> 6893      SVN      CHN 2000    12.574958    12.716478 1.0118017 1.0116019
#> 4801      LUX      ESP 2000   499.658201   499.641771 1.0002503 1.0002389
#> 1605      CZE      CAN 2000    93.113561    91.955797 1.0099827 1.0099972
#> 3573      IDN      EST 2000     1.509861     1.460711 0.9999865 0.9999931
#> 2809      FRA      TWN 2000  2339.693451  2336.041658 1.0001980 1.0001950
#> 6085      PRT      KOR 2000    13.042367    13.041252 1.0000813 1.0000725
#> 3869      IND      USA 2000 10715.495243 10715.810196 0.9999966 0.9999961
#>       nom_wage price_index
#> 6429 0.9998898   0.9999143
#> 485  1.0002030   0.9998443
#> 5629 1.0001322   0.9998266
#> 6893 0.9970762   0.9856409
#> 4801 1.0001388   0.9998999
#> 1605 1.0030564   0.9931279
#> 3573 0.9998933   0.9999002
#> 2809 1.0002656   1.0000706
#> 6085 0.9998933   0.9998208
#> 3869 0.9999125   0.9999164

This assumes a standard trade elasticity value of \(\theta = 4\). The input for \(\beta\) is given by the variable we created called eu_effect, which is equal to 0.224 for new EU pairs formed during the period and equal to 0 otherwise. Because of the small size of the sample, it solves almost instantly. Sample results for the first 10 rows in the data are shown above for the counterfactual trade level and the associated changes in welfare, real wages, nomimal wages, and the local price index. Click on the right arrow to scroll to the right if they are not all displayed above. For the latter four variables, the number shown is the result computed for the exporting country. Unsurprisingly, the new EU members (Bulgaria, Croatia, Czech Republic, Estonia, Hungary, Latvia, Lithuania, Malta, Poland, Romania, Slovakia, and Slovenia) realize the largest welfare gains from their joining the EU, with existing EU countries also gaining. All countries not included in the agreement experience small losses due to trade diversion, with the largest losses accruing to Russia.

We can also change how trade imbalances enter the model. The default (exibited above with mult = FALSE) is to assume that they enter expenditure additively (i.e., \(E_j = Y_j + D_j\)), but one can also change the model so that expenditure is instead a fixed multiple of income (i.e., let \(E_j = \delta_j Y_j\).) by setting mult = TRUE. While using multiplicative imbalances instead of additive balances changes the results slightly, they are still qualitatively very similar.

An important point about the above exercises is that the initial partial effect is estimated with some uncertainty. The GE results that were calculated may paint a misleading picture because they do not take this uncertainty into account. For this reason, it is considered good practice to use a bootstrap method to construct confidence intervals for the GE calculations. This type of procedure can be made easier using ge_gravity function:

library(data.table)  # needed below for bootstrap procedure

# Helper function for shuffling the data with replacement.
# This allows us to shuffle by pair rather than treating each observation as independent.
get_bootdata <- function(data=list(),id) {
  uniq_id <- levels(factor(data[,id]))
  draw    <- sort(sample(uniq_id,replace=TRUE))
  draw  <- data.table(draw)[,.N,by=draw]  # count duplicate pairs in bootstrap sample
  colnames(draw)[1] <- id
  boot_data  <- merge(data,draw,"pair",all.x=FALSE,all.y=FALSE)
  boot_index <- rep(row.names(boot_data), boot_data$N)  # replicates pairs drawn multiple times after merge
  boot_data  <- boot_data[matrix(boot_index), ]
  boot_data$rep <- (as.numeric(rownames(boot_data)) %% 1)*10+1
  return(data.frame(boot_data))
}

# set up for pair bootstrap
set.seed(12345)
bootreps      <- 20
TradeData0014[,"pair"] <- interaction(TradeData0014$expcode,TradeData0014$impcode) # This is the ID we will use for resampling.

# Initialize matrices for saving results
x             <- TradeData0014[,c("eu_enlargement","other_fta")]
save_partials <- matrix(nrow = bootreps, ncol = ncol(x), dimnames = list(1:bootreps,colnames(x)))
GE_effects    <- ge_results[,11:15]
save_GE       <- matrix(nrow = bootreps, ncol = ncol(GE_effects), dimnames = list(1:bootreps,colnames(GE_effects)))

# generate bootstrapped gravity estimates using alpaca's feglm function (20 boot reps)
library(alpaca)
for (b in 1:bootreps) {
    
    # This step shuffles the data using the get_bootdata() function defined above
    boot_data <- get_bootdata(TradeData0014,"pair")
    
    # These next few steps are exactly the same as the ones we used above to estimate the partial effects
    
    # Generate foreign trade subset
    f_trade <- boot_data[boot_data$exporter != boot_data$importer,]

    # classify FEs to be absorbed
    f_trade$exp_year <- interaction(f_trade$expcode, f_trade$year)
    f_trade$imp_year <- interaction(f_trade$impcode, f_trade$year)
    f_trade$pair     <- interaction(f_trade$impcode, f_trade$expcode)
    
    # Estimate and save partial effects
    save_partials[b,] <- feglm(
    formula = trade ~ eu_enlargement + other_fta | exp_year + imp_year + pair,
    data    = f_trade,
    family  = poisson()
    )$coefficient  # We just need the coefficients for computation
}

# Obtain bootstrapped GE results based on bootstrapped partial effects
bootstrap_GE_results <- ge_baseline_data
for (b in 1:bootreps) {
  
  # set up baseline data using the estimated partial effect from bootstrap b
  boot_ge_data <- ge_baseline_data
  boot_ge_data$eu_effect <- save_partials[b,1] * boot_ge_data$new_eu_pair 
  
  # run GE_gravity
  temp <- ge_gravity(
  exp_id = boot_ge_data$expcode,    # Origin country associated with each observation
  imp_id = boot_ge_data$impcode,    # Destination country associated with each observation
  flows  = boot_ge_data$trade,      # Observed trade flows in the data for the year being used as the baseline
  beta   = boot_ge_data$eu_effect,  # “Partial” change in trade, obtained as coefficient from gravity estimation
  theta  = 4,               # Trade elasticity
  mult   = FALSE,           # Assume trade balance is an additive component of national expenditure
  data   = boot_ge_data
  )
  
  # store results
  bootstrap_GE_results[,paste0("welf",b)] <- temp[,"welfare"]
  bootstrap_GE_results[,paste0("trade",b)] <- temp[,"new_trade"]
}

# get bootstrapped means, SDs, and 95% CIs for partial effects
colMeans(save_partials)
#> eu_enlargement      other_fta 
#>     0.24045195    -0.03465284
apply(save_partials, 2, sd)
#> eu_enlargement      other_fta 
#>     0.07753165     0.05578904
apply(save_partials, 2, function(x) quantile(x, probs = .975))
#> eu_enlargement      other_fta 
#>     0.34988358     0.05572457
apply(save_partials, 2, function(x) quantile(x, probs = .025))
#> eu_enlargement      other_fta 
#>     0.09867022    -0.11837670

# Get 95% CIs for GE effects
temp <- bootstrap_GE_results[,12:51]
temp <- temp[,order(colnames(temp))]

bootstrap_GE_results[,"lb_welf"] <- apply(temp[,21:40], 1, function(x) quantile(x, probs = .025))
bootstrap_GE_results[,"ub_welf"] <- apply(temp[,21:40], 1, function(x) quantile(x, probs = .975))
bootstrap_GE_results[,"lb_trade"] <- apply(temp[,1:20], 1, function(x) quantile(x, probs = .025))
bootstrap_GE_results[,"ub_trade"] <- apply(temp[,1:20], 1, function(x) quantile(x, probs = .975))

disp_cols <- c("exporter","importer","year","trade","lb_welf","ub_welf","lb_trade","ub_trade")
bootstrap_GE_results[sample(1:nrow(ge_results), 10),disp_cols] # 10 random rows; GE welfare effects are for *exporter*
#>      exporter importer year        trade   lb_welf   ub_welf     lb_trade
#> 1149      CHE      ITA 2000 7.749205e+03 0.9999020 0.9999746 7.752873e+03
#> 4017      IRL      ROW 2000 1.639069e+04 1.0000977 1.0003829 1.635859e+04
#> 1557      CYP      RUS 2000 1.165478e+01 1.0035637 1.0141773 1.174513e+01
#> 3605      IDN      IND 2000 1.156623e+03 0.9999779 0.9999943 1.156626e+03
#> 5197      MEX      ITA 2000 3.174025e+02 0.9999928 0.9999981 3.175410e+02
#> 5449      MLT      TWN 2000 9.318681e-01 1.0063494 1.0255347 9.040972e-01
#> 1093      CHE      CZE 2000 3.707880e+02 0.9999020 0.9999746 3.564777e+02
#> 497       BEL      ROW 2000 2.142915e+04 1.0001526 1.0006022 2.138667e+04
#> 7581      USA      BGR 2000 1.377859e+02 0.9999968 0.9999992 1.225898e+02
#> 6737      SVK      ESP 2000 7.114036e+01 1.0038431 1.0153599 7.871396e+01
#>          ub_trade
#> 1149 7.761856e+03
#> 4017 1.638199e+04
#> 1557 1.193969e+01
#> 3605 1.156631e+03
#> 5197 3.178676e+02
#> 5449 9.254744e-01
#> 1093 3.670091e+02
#> 497  2.141733e+04
#> 7581 1.334064e+02
#> 6737 1.012978e+02

Note again that the displayed bounds on welfare estimates refer to welfare changes for the exporting country.

Program Execution

Instead of calling the function, let’s assume that we have the variables set as following:

exp_id <- ge_baseline_data$expcode
imp_id <- ge_baseline_data$impcode
flows  <- ge_baseline_data$trade
beta   <- ge_baseline_data$eu_effect
theta  <- 4
mult   <- FALSE

In the following, we are going to trace and test the algorithm as if it were being called.

As an assumption: - \(i\) indices are defined for each origin/exporter, and matrices enumerable by them are Nx1 matrices. Sums for all \(i\) are generally defined by colSums - \(j\) indices are defined for each destination/importer, and matrices enumerable by them are 1xN matrices. Sums for all \(j\) are generally defined by rowSums - Column- and Row-wise summations will be done explicitly, and R’s vector math operations will not be assumed to facilitate it.

To be safe and explanatory, we will also define a few functions: - Typesafe function ts that can verify that our initial dimensions hold and that no \(\texttt{NA}\) values are introduced. - Sanity function sanity that will make sure that a vector/matrix does not change cardinality illogically. - printHead to show only a tiny subset of data without much code.

printHead <- function(Vec, rows = 6, cols = 6) {
  print(Vec[1:min(rows, nrow(Vec)), 1:min(cols, ncol(Vec))])
}

ts <- function(Vec, Val, line = "?") {
  if (dim(Vec)[1] != dim(Val)[1] && dim(Vec)[2] != dim(Val)[2]) {
    warning(paste(" > Assigned vector has improper dimensions on line", line, "\n"))
    message("Assigning value: \n")
    printHead(Val)
    message("To Value: \n")
    printHead(Vec)
    if (readline() == "q") return()
  }
  if (anyNA(Val)) {
    warning(paste(" > Assigned vector has NAs on line", line, "\n"))
    printHead(Val)
    if (readline() == "q") return()
  }
  return(Val)
}

sanity <- function(name, Vec, dstr) {
  message(" > Sanity Check: ")
  for (i in 1:length(Vec))
    message("  - dim(", name[i], ") = ",
      dim(Vec[[i]])[1], " x ", dim(Vec[[i]])[2],
      " (defined for ", dstr[i], ")"
    )
}

Let us first set up the set of international trade flows matrix, \(X_{ij}\) (w/ \(i\) exporting to \(j\)). This is just the set of flows arranged in an exporter (rows) by importer (columns) fashion.

X   <- flows
n   <- sqrt(length(X))        # Length of row or column of trade matrix
X   <- t(matrix(flows, n, n)) # Square the matrix
printHead(X)
#>              [,1]         [,2]        [,3]        [,4]         [,5]
#> [1,] 7.047775e+05     61.95446    345.4675     5.71090 5.577426e+02
#> [2,] 3.658264e+02 261390.90409   1224.3476   144.50709 2.635246e+02
#> [3,] 4.753819e+02   1516.67071 343253.2434    68.76933 4.872147e+02
#> [4,] 7.448854e-01     17.67560    111.4472 25137.17943 1.040889e+00
#> [5,] 4.858000e+02    221.86748   1308.2011    47.55200 1.086039e+06
#> [6,] 1.437038e+03    659.92572   1136.6122     7.58329 8.533425e+02
#>              [,6]
#> [1,] 1.583679e+03
#> [2,] 8.459328e+02
#> [3,] 6.059549e+02
#> [4,] 1.269456e+01
#> [5,] 8.835362e+02
#> [6,] 1.066313e+06

Then, set \({\texttt B} \ (= e^{\beta})\) to be the matrix of partial effects. Notice that the diagonal must be set to 0.

B <- beta
dim(B)  <- c(n, n) # Format B to have K.n columns
diag(B) <- 0       # Set diagonal to 0 (this is required and is corrected if found)
B <- exp(B)
printHead(B)
#>      [,1]     [,2]     [,3]     [,4] [,5] [,6]
#> [1,]    1 1.000000 1.000000 1.000000    1    1
#> [2,]    1 1.000000 1.000000 1.251383    1    1
#> [3,]    1 1.000000 1.000000 1.251383    1    1
#> [4,]    1 1.251383 1.251383 1.000000    1    1
#> [5,]    1 1.000000 1.000000 1.000000    1    1
#> [6,]    1 1.000000 1.000000 1.000000    1    1

Now, we can set up some more variables:

Let \(E_j\) be the Total National Expendatures for country \(j\) such that \(E_j \equiv \sum_i X_{ij}\).
Let \(Y_j\) be the Total Labor Income for country \(i\) such that \(Y_i \equiv w_iL_j = \sum_j X_{ij}\).
Let \(D_j\) be the National Trade Deficit for country \(j\) such that \(D_j \equiv E_j - Yj\).

# Set up Y, E, D vectors; calculate trade balances
E <- matrix(colSums(X), n, 1) # Total National Expendatures; Value of import for all origin
Y <- matrix(rowSums(X), n, 1) # Total Labor Income; Value of exports for all destinations;
D <- E - Y                    # D: National trade deficit / surplus

sanity(c("E","Y","D"), list(E, Y, D), c("j","j","j"))
#>  > Sanity Check:
#>   - dim(E) = 44 x 1 (defined for j)
#>   - dim(Y) = 44 x 1 (defined for j)
#>   - dim(D) = 44 x 1 (defined for j)

Then we set up the \(\pi_{ij}\) matrix of bilateral trade shares such that \(\pi_{ij} = X_{ij}/E_{j}\):

# set up pi_ij matrix of trade shares; pi_ij = X_ij/E_j
Pi <- X / kronecker(t(E), matrix(1,n,1))  # Bilateral trade share
sanity(c("X"), list(X), c("i and j"))
#>  > Sanity Check:
#>   - dim(X) = 44 x 44 (defined for i and j)

Now, we are almost done. In this model, we want to build up:

The change in price levels in each country \(\hat{P_j}\) for all exporters.
The change in welfare \(\hat{W}_{j}\) for all exporters.
The general equilibrium trade impact (GETI) \(\hat{X}_{ij}\) between all exporters and importers.

The iterative algorithm provided will build these up iteratively, starting them off as 1-column matrices.

w_hat <- P_hat <- matrix(1, n, 1)   # Containers for running w_hat and P_hat
X_new <- X                          # Container for updated X
sanity(c("w_hat", "P_hat"), list(w_hat, P_hat), c("i", "i"))
#>  > Sanity Check:
#>   - dim(w_hat) = 44 x 1 (defined for i)
#>   - dim(P_hat) = 44 x 1 (defined for i)

Loop Processes

Step 1: Update \(\hat{w}_i\) for all origins using formula:

\[\widehat{w}_{i} =\left[Y_{i}^{-1}\sum_{j}\frac{\pi_{ij}\cdot e^{\beta\times FTA_{ij}}}{\widehat{P}_{j}^{-\theta}}\cdot E_{j}^{\prime}\right]^{\frac{1}{1+\theta}}\quad\forall i.\]

eqn_base <- ((Pi * B) %*% (E / P_hat)) / Y
w_hat    <- ts(w_hat, eqn_base^(1/(1+theta)))

Step 2: Normalize so total world output stays the same:

\(\sum_{i}Y_{i}\widehat{w}_{i}=\sum_{i}Y_{i}\).

w_hat <- ts(w_hat, w_hat * (sum(Y) / sum(Y*w_hat)))

Step 3: Update

\(\widehat{P}_{j}^{-\theta}=\left[\sum_{k}\pi_{kj}\widehat{w}_{k}^{-\theta}e^{b\times FTA_{kj}}\right] \forall \ j\).

P_hat <- ts(P_hat, (t(Pi) * t(B)) %*% (w_hat^(-theta)))

Step 4: Update

\(E_{j}^{\prime}=Y_{j}\widehat{w}_{j}+D_{j} \ \forall \ j\).

if (mult) {
  E = ts(E, (Y + D) * w_hat)
} else {
  # default is to have additive trade imbalances
  E = ts(E, Y * w_hat + D)
}

Calculate new trade shares (to verify convergence)

p1 <- (Pi * B)
p2 <- kronecker((w_hat^(-theta)), matrix(1,1,n))
p3 <- kronecker(t(P_hat), matrix(1,n,1))

Pi_new <- ts(Pi, p1 * p2 / p3, 296)

X_new <- ts(X, Pi_new * kronecker(t(E), matrix(1,n,1)))

From there, we just need a way to check convergence to a steady-state, so let’s put it all together:

# Initialize w_i_hat = P_j_hat = 1
w_hat <- P_hat <- matrix(1, n, 1)    # Wi = Ei/Pi

# While Loop Initializations
X_new     <- X         # Container for updated X
crit      <- 1         # Convergence testing value
curr_iter <- 0         # Current number of iterations
max_iter  <- 1000000   # Maximum number of iterations
tol       <- .00000001 # Threshold before sufficient convergence

# B = i x j
# D = 1 x j
# E = 1 x j
# w_hat = P_hat = i x 1
# Y = E = D = i x 1

repeat { # Event Loop (using repeat to simulate do-while)

  X_last_step <- X_new

  #### Step 1: Update w_hat_i for all origins:
  eqn_base <- ((Pi * B) %*% (E / P_hat)) / Y
  w_hat    <- eqn_base^(1/(1+theta))

  #### Step 2: Normalize so total world output stays the same
  w_hat <- w_hat * (sum(Y) / sum(Y*w_hat))

  #### Step 3: update P_hat_j
  P_hat <- (t(Pi) * t(B)) %*% (w_hat^(-theta))

  #### Step 4: Update $E_j$
  if (mult) {
    E <- (Y + D) * w_hat
  } else {
    E <- Y * w_hat + D  # default is to have additive trade imbalances
  }

  #### Calculate new trade shares (to verify convergence)
  p1 <- (Pi * B)
  p2 <- kronecker((w_hat^(-theta)), matrix(1,1,n))
  p3 <- kronecker(t(P_hat), matrix(1,n,1))
  Pi_new <- p1 * p2 / p3

  X_new <- t(Pi_new * kronecker(t(E), matrix(1,n,1)))

  # Compute difference to see if data converged
  crit = max(c(abs(log(X_new) - log(X_last_step))), na.rm = TRUE)
  curr_iter <- curr_iter + 1

  if(crit <= tol || curr_iter >= max_iter)
    break
}

From here, we can just aggregate statistics, based in part with the formulas:

\[ \begin{alignat}{1} \textbf{GE Welfare Impact}:\quad & \widehat{W}_{i}=\widehat{E}_{i}/\widehat{P}_{i}\\ \\ \textbf{GE Real Wage Impact}:\quad & \widehat{rw}_{ij}=\widehat{w}_{i}/\widehat{P}_{i},\\ \textbf{GE Trade Impact}:\quad & \widehat{X}_{ij}=\frac{\widehat{w}_{i}^{-\theta}e^{\beta\times FTA_{ij}}}{\widehat{P}_{j}^{-\theta}}\cdot\widehat{E}_{j} \end{alignat} \]

# Post welfare effects and new trade values
dim(X_new) <- c(n*n, 1)

# Real wage impact
real_wage  <- w_hat / (P_hat)^(-1/theta)
# real_wage <- (diag(Pi_new) / diag(Pi))^(-1/theta)  # (ACR formula)

# Welfare impact
if (mult) {
  welfare <- real_wage
} else {
  welfare <- ((Y * w_hat) + D) / (Y+D) / (P_hat)^(-1/theta)
}

# Kronecker w/ this creates n dupes per dataset in column to align with X matrix
kron_base <- matrix(1, n, 1)

welfare     <- kronecker(welfare, kron_base)
real_wage   <- kronecker(real_wage, kron_base)
nom_wage    <- kronecker(w_hat, kron_base)

price_index <- kronecker(((P_hat)^(-1/theta)), kron_base)

And then, we can just return them:

# Build and return the final list
data_out <- ge_baseline_data

data_out$new_trade   <- X_new
data_out$welfare     <- welfare
data_out$real_wage   <- real_wage
data_out$nom_wage    <- nom_wage
data_out$price_index <- price_index

head(data_out[,c(1:2,5:6,12:16)])
#>    exporter importer year        trade    new_trade   welfare real_wage
#> 1       AUS      AUS 2000 704777.47410 7.047388e+05 0.9999938 0.9999945
#> 5       AUS      AUT 2000     61.95446 6.200899e+01 0.9999938 0.9999945
#> 9       AUS      BEL 2000    345.46746 3.454304e+02 0.9999938 0.9999945
#> 13      AUS      BGR 2000      5.71090 5.302484e+00 0.9999938 0.9999945
#> 17      AUS      BRA 2000    557.74257 5.576790e+02 0.9999938 0.9999945
#> 21      AUS      CAN 2000   1583.67895 1.583680e+03 0.9999938 0.9999945
#>     nom_wage price_index
#> 1  0.9999236   0.9999292
#> 5  0.9999236   0.9999292
#> 9  0.9999236   0.9999292
#> 13 0.9999236   0.9999292
#> 17 0.9999236   0.9999292
#> 21 0.9999236   0.9999292

Running The Algorithm

Pre-Processing

# Foreign trade subset
f_trade <- TradeData0014[TradeData0014$exporter != TradeData0014$importer,]

# Normalize trade data to unit interval
f_trade$trade <- f_trade$trade / max(f_trade$trade)

# classify FEs for components to be absorbed (finding variable interactions)
f_trade$exp_year <- interaction(f_trade$expcode, f_trade$year)
f_trade$imp_year <- interaction(f_trade$impcode, f_trade$year)
f_trade$pair     <- interaction(f_trade$impcode, f_trade$expcode)

# Fit generalized linear model based on specifications
partials <- feglm(
  formula = trade ~ eu_enlargement + other_fta | exp_year + imp_year + pair,
  data    = f_trade,
  family  = poisson()
)$coefficient  # We just need the coefficients for computation

# Sort trade matrix to make it easier to find imp/exp pairs
t_trade <- TradeData0014[order(
  TradeData0014$exporter,
  TradeData0014$importer,
  TradeData0014$year
),]

t_trade$eu_effect <- NA      # this creates a new column with the partial effect of EU membership for new EU pairs
i <- 1
# Effect of EU entrance on country based on partial, if entry happened
invisible(by(t_trade, list(t_trade$expcode, t_trade$impcode), function(row) {
  # Was a new EU pair created within time span?
  t_trade[i:(i+nrow(row)-1), "eu_effect"] <<- diff(row$eu_enlargement, lag=nrow(row)-1)
  i <<- i + nrow(row)
}))
# If added to EU, give it the computed partial eu_enlargement coefficient as the effect
t_trade$eu_effect = t_trade$eu_effect * partials[1]

# Data to be finally fed to the function
data <- t_trade[t_trade$year == 2000,]   # In example, 1892 Entries, 5676 removed
head(data)
#>    exporter importer expcode impcode year        trade eu_enlargement other_fta
#> 1       AUS      AUS       1       1 2000 704777.47410              0         1
#> 5       AUS      AUT       1       2 2000     61.95446              0         0
#> 9       AUS      BEL       1       3 2000    345.46746              0         0
#> 13      AUS      BGR       1       4 2000      5.71090              0         0
#> 17      AUS      BRA       1       5 2000    557.74257              0         0
#> 21      AUS      CAN       1       6 2000   1583.67895              0         0
#>    FTA pair eu_effect
#> 1    1  1.1         0
#> 5    0  1.2         0
#> 9    0  1.3         0
#> 13   0  1.4         0
#> 17   0  1.5         0
#> 21   0  1.6         0

Running Actual Computations

## Difference between w_mult and w_o_mult is how trade balance is considered
## mult = TRUE assumes multiplicative trade balances; false assumes additive

w_mult <- ge_gravity(
  exp_id = data$expcode,    # Origin country associated with each observation
  imp_id = data$impcode,    # Destination country associated with each observation
  flows  = data$trade,      # Observed trade flows in the data for the year being used as the baseline
  beta   = data$eu_effect,  # “Partial” change in trade, obtained as coefficient from gravity estimation
  theta  = 4,               # Trade elasticity
  mult   = TRUE,            # Assume trade balance is a multiplicative component of national expenditure
  data   = data
)

w_o_mult <-  ge_gravity(
  exp_id = data$expcode,    # Origin country associated with each observation
  imp_id = data$impcode,    # Destination country associated with each observation
  flows  = data$trade,      # Observed trade flows in the data for the year being used as the baseline
  beta   = data$eu_effect,  # “Partial” change in trade, obtained as coefficient from gravity estimation
  theta  = 4,                # Trade elasticity
  mult   = FALSE,           # Assume trade balance is an additive component of national expenditure
  data   = data
)

Final results without multiplication parameter

head(w_o_mult)
#>    exporter importer expcode impcode year        trade eu_enlargement other_fta
#> 1       AUS      AUS       1       1 2000 704777.47410              0         1
#> 5       AUS      AUT       1       2 2000     61.95446              0         0
#> 9       AUS      BEL       1       3 2000    345.46746              0         0
#> 13      AUS      BGR       1       4 2000      5.71090              0         0
#> 17      AUS      BRA       1       5 2000    557.74257              0         0
#> 21      AUS      CAN       1       6 2000   1583.67895              0         0
#>    FTA pair eu_effect    new_trade   welfare real_wage  nom_wage price_index
#> 1    1  1.1         0 7.047388e+05 0.9999938 0.9999945 0.9999236   0.9999292
#> 5    0  1.2         0 6.200899e+01 0.9999938 0.9999945 0.9999236   0.9999292
#> 9    0  1.3         0 3.454304e+02 0.9999938 0.9999945 0.9999236   0.9999292
#> 13   0  1.4         0 5.302484e+00 0.9999938 0.9999945 0.9999236   0.9999292
#> 17   0  1.5         0 5.576790e+02 0.9999938 0.9999945 0.9999236   0.9999292
#> 21   0  1.6         0 1.583680e+03 0.9999938 0.9999945 0.9999236   0.9999292

Final results with multiplication parameter

head(w_mult)
#>    exporter importer expcode impcode year        trade eu_enlargement other_fta
#> 1       AUS      AUS       1       1 2000 704777.47410              0         1
#> 5       AUS      AUT       1       2 2000     61.95446              0         0
#> 9       AUS      BEL       1       3 2000    345.46746              0         0
#> 13      AUS      BGR       1       4 2000      5.71090              0         0
#> 17      AUS      BRA       1       5 2000    557.74257              0         0
#> 21      AUS      CAN       1       6 2000   1583.67895              0         0
#>    FTA pair eu_effect    new_trade   welfare real_wage  nom_wage price_index
#> 1    1  1.1         0 7.047407e+05 0.9999948 0.9999948 0.9999268   0.9999321
#> 5    0  1.2         0 6.200460e+01 0.9999948 0.9999948 0.9999268   0.9999321
#> 9    0  1.3         0 3.454142e+02 0.9999948 0.9999948 0.9999268   0.9999321
#> 13   0  1.4         0 5.261708e+00 0.9999948 0.9999948 0.9999268   0.9999321
#> 17   0  1.5         0 5.576743e+02 0.9999948 0.9999948 0.9999268   0.9999321
#> 21   0  1.6         0 1.583683e+03 0.9999948 0.9999948 0.9999268   0.9999321

Comparison with Stata Counterpart

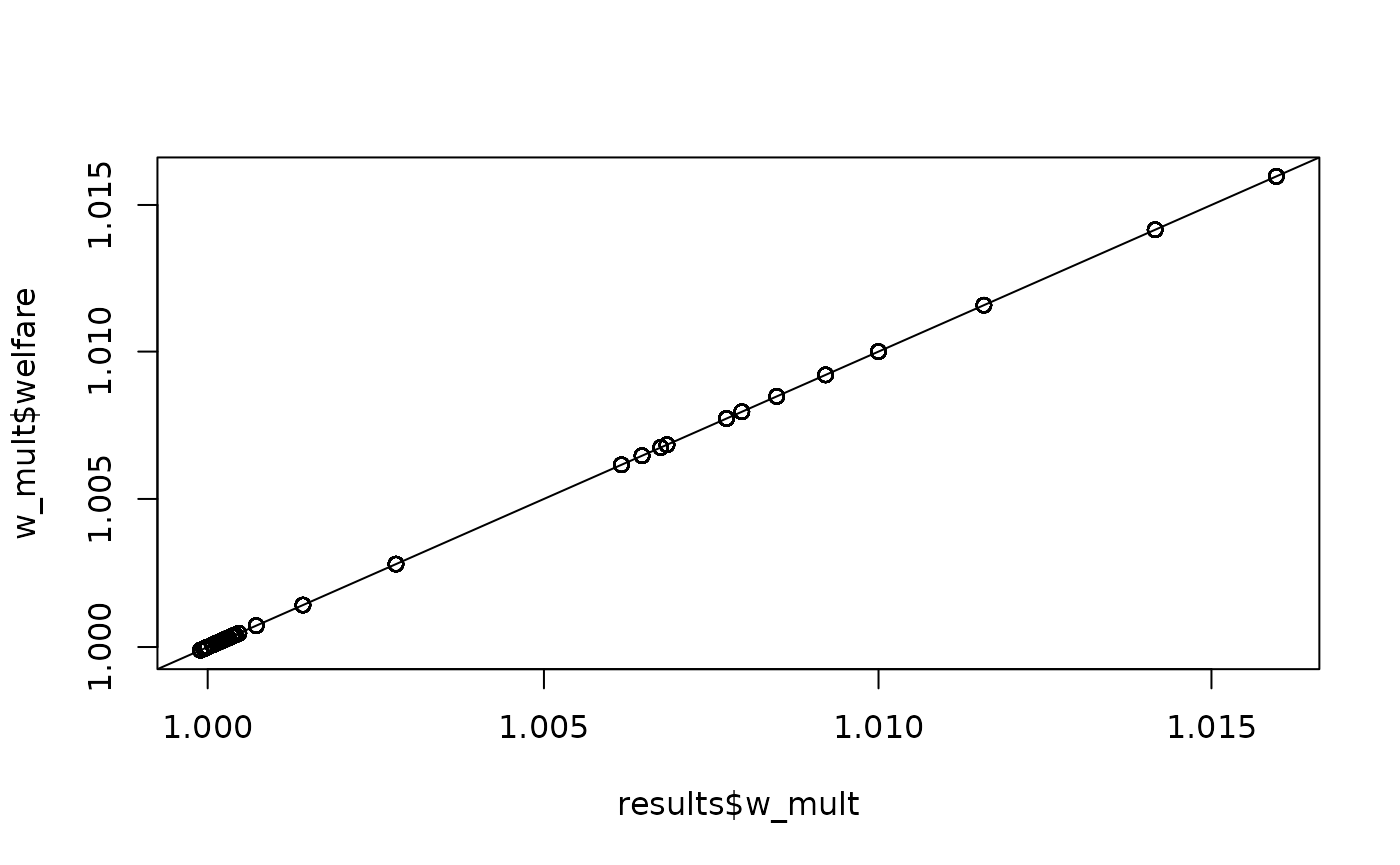
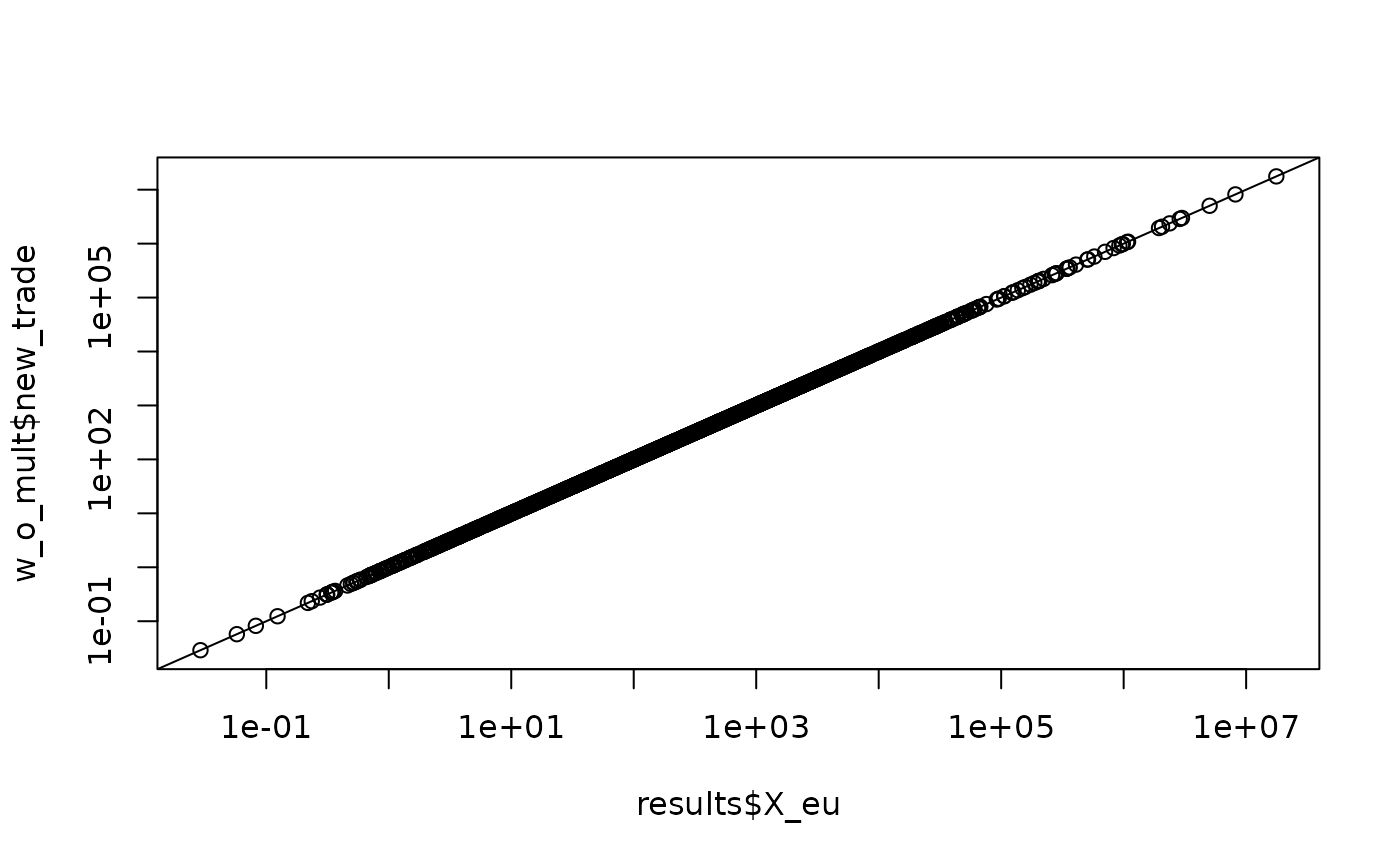
Before running comparisons, we need to slightly modify the results data to sync with our new format.

# Notice that the Stata counterpart returned all years with a sparse
# selection labeled with computed values. Ours just returns the new data
# by default or tags it onto the data provided in the `data` parameter.

# To make it sync, just extract a year.
results <- TradeData0014_Results[TradeData0014_Results$year == 2000, ]
head(results)
#>    exporter importer expcode impcode year        trade eu_enlargement other_fta
#> 1       AUS      AUS       1       1 2000 704777.47410              0         1
#> 5       AUS      AUT       1       2 2000     61.95446              0         0
#> 9       AUS      BEL       1       3 2000    345.46746              0         0
#> 13      AUS      BGR       1       4 2000      5.71090              0         0
#> 17      AUS      BRA       1       5 2000    557.74257              0         0
#> 21      AUS      CAN       1       6 2000   1583.67895              0         0
#>    FTA new_eu_pair eu_effect      w_eu         X_eu    w_mult       X_mult
#> 1    1           0         0 0.9999938 7.047388e+05 0.9999948 7.047407e+05
#> 5    0           0         0 0.9999938 6.200899e+01 0.9999948 6.200460e+01
#> 9    0           0         0 0.9999938 3.454304e+02 0.9999948 3.454142e+02
#> 13   0           0         0 0.9999938 5.302484e+00 0.9999948 5.261708e+00
#> 17   0           0         0 0.9999938 5.576790e+02 0.9999948 5.576743e+02
#> 21   0           0         0 0.9999938 1.583680e+03 0.9999948 1.583683e+03

Comparison of w_eu from results to the welfare w/o multiplier

plot(x = results$w_eu, y = w_o_mult$welfare, log = "xy")
abline(coef = c(0,1))


message("Max difference: ", max(abs(results$w_eu - w_o_mult$welfare)))
#> Max difference: 5.84207948683968e-08

Comparison of w_mult from results to the welfare with multiplier

plot(x = results$w_mult, y = w_mult$welfare, log = "xy")
abline(coef = c(0,1))


message("Max difference: ", max(abs(results$w_mult - w_mult$welfare)))
#> Max difference: 5.82429970918952e-08

Comparing results of new X w/o multiplier option

plot(x = results$X_eu, y = w_o_mult$new_trade, log = "xy")
abline(coef = c(0,1))


message("Max difference: ", max(abs(results$X_eu - w_o_mult$new_trade)))
#> Max difference: 0.217820517718792

Comparing results of new X with multiplier option

plot(x = results$X_mult, y = w_mult$new_trade, log = "xy")
abline(coef = c(0,1))


message("Max difference: ", max(abs(results$X_mult - w_mult$new_trade)))
#> Max difference: 0.472535479813814

Advisory

This is an advanced technique that requires a basic understanding of the model being solved. I would recommend reading either Section 4.3 of Head & Mayer (2014) or Ch. 2 of Yotov, Piermartini, Monteiro, & Larch (2016) before implementing.

One common issue that researchers new to these methods should be aware of is that GE trade models require a “square” data set with information on internal trade flows in addition to data on international trade flows. In the model, these internal flows are denoted by \(X_{ii}\). If ge_gravity detects that the variable given for does not include one or more \(X_{ii}\) terms, it will exit with an error. Not all publicly available trade data sets include internal trade values. But some that do include WIOD, Eora MRIO, and the data set made available by UNCTAD as part of their online course on trade policy analysis (see Yotov, Piermartini, Monteiro, & Larch, 2016.)

Depending on interest, future versions could feature additional options such as allowances for tariff revenues and/or multiple sectors. If you believe you have found an error that can be replicated, or have other suggestions for improvements, please feel free to
contact me.

Acknowledgements

The basic idea of using fixed point iteration to solve the gravity model has previously been implemented in Stata by Head & Mayer (2014) and Anderson, Larch, & Yotov (2015). Funding for this R package was provided by the Department for Digital, Culture, Media and Sport, United Kingdom.

Suggested citation

If you are using this command in your research, please cite

Baier, Scott L., Yoto V. Yotov, and Thomas Zylkin. “On the widely differing effects of free trade agreements: Lessons from twenty years of trade integration”. Journal of International Economics 116 (2019): 206-226.

The algorithm used in this command was specifically written for the exercises performed in this paper. Section 6 of the paper provides a more detailed description of the underlying model and its connection to the literature.